
In fact, the column space and nullspace are intricately connected by the rank-nullity theorem, which in turn is part of the fundamental theorem of linear algebra. Properties (a), (b), and (c) guarantee that a H of V is itself a vector space, under the linear space operations already defined in V. For each u in H and each number c, cu is in H. This establishes that the nullspace is a vector space as well. A subspace is any set in R n that has three properties: Another way of stating properties 2 and 3 is that is closed under addition and scalar. SUBSPACES Definition: A subspace of a vector space V is a subset H of V that has three properties: a. For instance, consider the set W W W of complex vectors v \mathbf \in N c v ∈ N for any scalar c c c. The 'rules' you know to be a subspace I'm guessing are 1) non-empty (or equivalently, containing the zero vector) 2) closure under addition 3) closure under scalar multiplication These were not chosen arbitrarily. We also present results regarding the coordination between students' concept image and how they interpret the formal definition, situations in which students recognized a need for the formal definition, and qualities of subspace that students noted were consequences of the formal definition.The simplest way to generate a subspace is to restrict a given vector space by some rule. The definition of a subspace is a subset that itself is a vector space. theorems form the building blocks of other results in linear algebra. If you think the above example as a subspace, then the subspace is inside some other (bigger or larger) vector space. You dont somehow end up with a vector thats outside of your set.
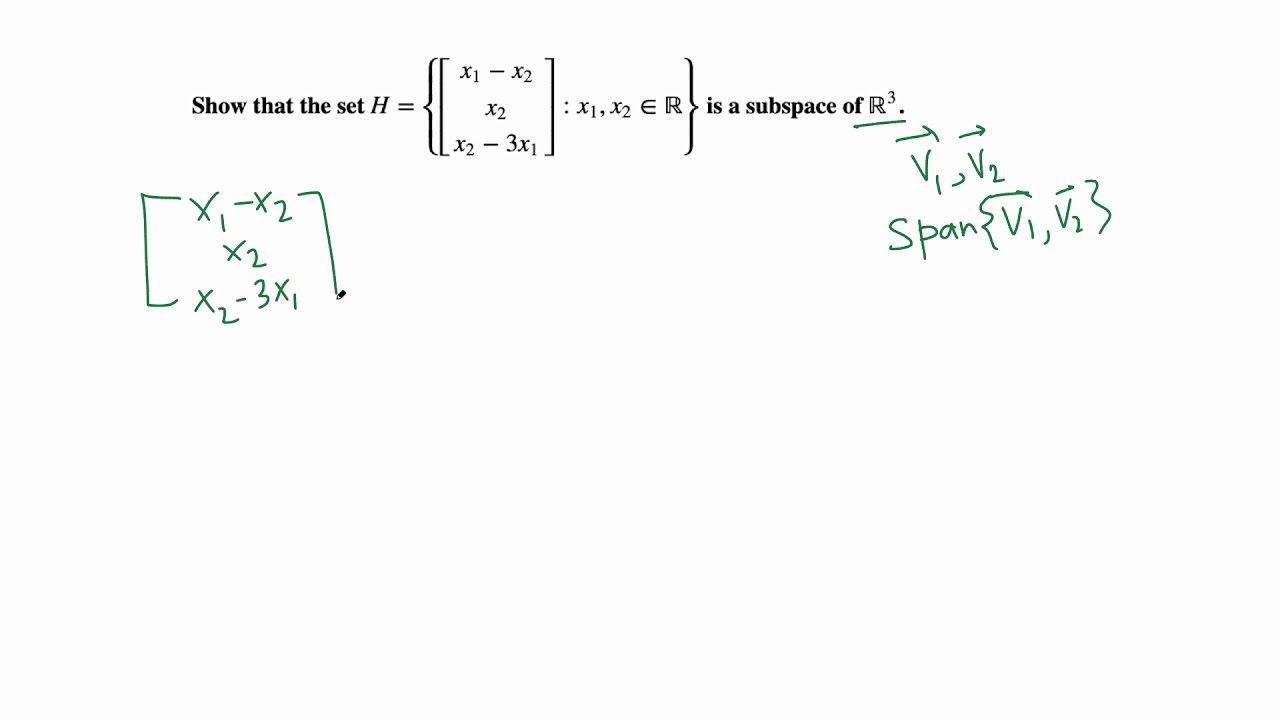
#Subspace definition linear algebra full
0 0 0/ is a subspace of the full vector space R3. Through grounded analysis, we identified recurring concept imagery that students provided for subspace, namely, geometric object, part of whole, and algebraic object. A wide variety of vector spaces are possible under the above definition as illus-. This illustrates one of the most fundamental ideas in linear algebra. A subspace is a subset that respects the two basic operations of linear algebra: vector addition and scalar multiplication.

We used the analytical tools of concept image and concept definition of Tall and Vinner (Educational Studies in Mathematics, 12(2): 151-169, 1981) in order to highlight this distinction in student responses. The idea this definition captures is that a subspace of V is a nonempty subset which is itself a vector space under the same addition and scalar multiplication. This is consistent with literature in other mathematical content domains that indicates that a learner's primary understanding of a concept is not necessarily informed by that concept's formal definition.

In interviews conducted with eight undergraduates, we found students' initial descriptions of subspace often varied substantially from the language of the concept's formal definition, which is very algebraic in nature. Prove that the image of a linear transformation is a subspace.

Define the image of a linear transformation. Decide whether a linear transformation is one-to-one or onto and how these questions are related to matrices. The 'rules' you know to be a subspace Im guessing are. Identify when a linear transformation is bijective. This paper reports on a study investigating students' ways of conceptualizing key ideas in linear algebra, with the particular results presented here focusing on student interactions with the notion of subspace. The definition of a subspace is a subset that itself is a vector space.


 0 kommentar(er)
0 kommentar(er)
